ASTB03 Assignment 1

ASTB03 Assignment 1                                                  Mark - 6110

    Eratosthenes was a Greek scientist who lived between 276 BC and 194 BC. After studying in Athens in his youth, he made significant contributions to the fields of math, geography, and astronomy. His friends nick-named him "Pentathlos" (an athlete who competes in 5 different sports), due to his nature of pursuing knowledge in a vast variety of fields. Considering the time, many of Eratosthenes accomplishments were remarkably revolutionary and accurate in their respective areas, and some are even used to this day.

    One such lasting impact by Eratosthenes is in mathematics. Eratosthenes proposed the first algorithm for finding prime numbers (numbers whose factors only include 1 and itself). The algorithm is known as "Sieve of Eratosthenes" and can be used to find all prime numbers between 1 and a given number. The algorithm involves the following steps:

1. Go through every number between 2 and the square root of the given number

2. If the current number is already crossed out, then skip it

3. If the current number is not crossed out, then take every multiple (2n, 3n, 4n, etc.) of that current number that is less than the given number and cross it out.

4. Once the algorithm has ran through every number up to the square root, the remaining uncrossed numbers are all of the prime numbers up to the given number.

For illustration, here is an example of the algorithm finding all prime numbers between 1-100.

For some cases, his proposed algorithm remains one of the most efficient ways to find prime numbers to this day. Prime numbers have very important applications in many fields, such as mathematics and computer science.

    Eratosthenes is also widely known as the father of geography. Using his understanding of the the dimensions of the Earth, Eratosthenes was able to form the first somewhat accurately labeled map of the known world at the time. Cataloging a series of past traveler's experiences, he used his knowledge of distances to create a (for the time) concise map of the world. With this map, Eratosthenes had created new conventions for measuring distance between locations. He used a mesh of grid lines running across the map both vertically and horizontally at equal distances to allow the user of the map to estimate how far another location is. This convention is still used to day, as maps will have lines running through them to represent latitude and longitude. Below is a reconstruction of the map that Eratosthenes created, which at the time included over 400 cities:

Although the map is obviously missing much of today's known world, considering knowledge at the time Eratosthenes did a fairly remarkable job in organizing the world into one accurate and effective map.

    Eratosthenes also spent some time studying chronology. He had the goal of using a scientific approach to catalog previous events in history. He organized important events in history from the siege of Troy (1194 BC) to his own era. On top of this, he also may have been the first person to invent a calendar that included a leap day (an extra day on some years that accounts for the non integer number of days in the earth's rotation around the sun).  Eratosthenes was also able to accurately measure the tilt of the earth. In addition,  Eratosthenes spent a significant amount of time cataloging stars (over 600 of them), and measuring the distance between the Sun/Moon and Earth. However, these measures were not as accurate as some of his other findings.

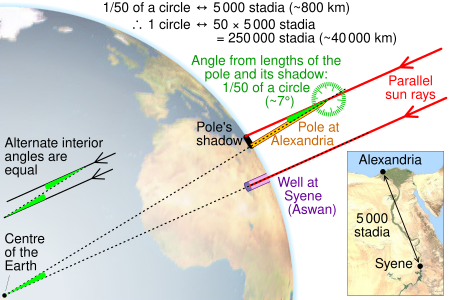
    Despite this impressive list of accomplishments, Eratosthenes' most impressive feat has yet to be mentioned. Eratosthenes was able to with high accuracy measure the circumference of the Earth. At the time, humans had yet to travel the entire planet, and thus had little understanding of the size of the earth beyond mapped out regions. This made precisely finding the circumference of the earth a difficult task, but Eratosthenes had a clever idea to do this. He knew that on one day each year (the summer solstice), in a particular spot (Syene) the rays of the sun shone perpendicular to a deep well. He knew this because the rays would hit the bottom of the well, but not the sides. Eratosthenes waited for this day, and then set up a pole in Alexandria which he knew from many detailed accounts was roughly 5000 stadia away. A stadia was a unit of measurement which is roughly 157.5 meters (Egyptian version). He then proceeded to measure the length of the pole, as well as the shadow it cast. Using basic trigonometry, he was able to measure the angle of the sun's rays, which he found to be roughly 7.2 degrees. Making the assumption that the Earth was spherical (360 degrees), he was then able to use all of this information to estimate the circumference of the Earth. Knowing that if he were to measure all the way around the earth, the angle would would have to go back to 0 degrees, he realized that the ratio of 360/7.2 would be same as the ratio between the circumference of the earth and the distance between the pole in Alexandra and the well in Syene. He thus did the simple algebra, solving for the circumference: cir = 360/7.2 * 5000 stadia = 250,000 stadia. There is some dispute over which value of stadia Eratosthenes used, but assuming he used the 157.5m version, his computed circumference in meters would be 39,375,000m. The actual circumference of the earth is roughly 40,075,000m, which means his findings were only off by about 2%. Considering his tools and the knowledge of the earth's geography at the time, this was an incredible and ingenious discovery. Below is an image which depicts the logic of the experiment:

Bibliography: 

https://www.britannica.com/biography/Eratosthenes

https://en.wikipedia.org/wiki/Eratosthenes

https://www.khanacademy.org/partner-content/big-history-project/solar-system-and-earth/knowing-solar-system-earth/a/eratosthenes-of-cyrene

https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes